Contents
- Model Training and Parameter Tuning
- Basic Parameter Tuning
- Customizing the Tuning Process
- Pre-Processing Options
- Alternate Tuning Grids
- Plotting the Resampling Profile
- The trainControl Function
- Alternate Performance Metrics
- Choosing the Final Model
- Extracting Predictions and Class Probabilities
- Exploring and Comparing Resampling Distributions
- Fitting Models Without Parameter Tuning
Model Training and Parameter Tuning
The caret package has several functions that attempt to streamline the model building and evaluation process.
The train function can be used to
- evaluate, using resampling, the effect of model tuning parameters on performance
- choose the "optimal" model across these parameters
- estimate model performance from a training set
First, a specific model must be chosen. Currently, 150 are available using caret; see train Model List or train Models By Tag for details. On these pages, there are lists of tuning parameters that can potentially be optimized. User-defined models can also be created.
The first step in tuning the model (line 1 in the algorithm above is to choose a set of parameters to evaluate. For example, if fitting a Partial Least Squares (PLS) model, the number of PLS components to evaluate must be specified.

Once the model and tuning parameter values have been defined, the type of resampling should be also be specified. Currently, k-fold cross-validation (once or repeated), leave-one-out cross-validation and bootstrap (simple estimation or the 632 rule) resampling methods can be used by train. After resampling, the process produces a profile of performance measures is available to guide the user as to which tuning parameter values should be chosen. By default, the function automatically chooses the tuning parameters associated with the best value, although different algorithms can be used (see details below below).
An Example
The Sonar data are available in the mlbench package. Here, we load the data:
library(mlbench) data(Sonar) str(Sonar[, 1:10])
'data.frame': 208 obs. of 10 variables: $ V1 : num 0.02 0.0453 0.0262 0.01 0.0762 0.0286 0.0317 0.0519 0.0223 0.0164 ... $ V2 : num 0.0371 0.0523 0.0582 0.0171 0.0666 0.0453 0.0956 0.0548 0.0375 0.0173 ... $ V3 : num 0.0428 0.0843 0.1099 0.0623 0.0481 ... $ V4 : num 0.0207 0.0689 0.1083 0.0205 0.0394 ... $ V5 : num 0.0954 0.1183 0.0974 0.0205 0.059 ... $ V6 : num 0.0986 0.2583 0.228 0.0368 0.0649 ... $ V7 : num 0.154 0.216 0.243 0.11 0.121 ... $ V8 : num 0.16 0.348 0.377 0.128 0.247 ... $ V9 : num 0.3109 0.3337 0.5598 0.0598 0.3564 ... $ V10: num 0.211 0.287 0.619 0.126 0.446 ...
The function createDataPartition can be used to create a stratified random sample of the data into training and test sets:
library(caret) set.seed(998) inTraining <- createDataPartition(Sonar$Class, p = 0.75, list = FALSE) training <- Sonar[inTraining, ] testing <- Sonar[-inTraining, ]
We will use these data illustrate functionality on this (and other) pages.
Basic Parameter Tuning
By default, simple bootstrap resampling is used for line 3 in the algorithm above. Others are availible, such as repeated K-fold cross-validation, leave-one-out etc. The function trainControl can be used to specifiy the type of resampling:
fitControl <- trainControl(## 10-fold CV method = "repeatedcv", number = 10, ## repeated ten times repeats = 10)
More information about trainControl is given in a section below.
The first two arguments to train are the predictor and outcome data objects, respectively. The third argument, method, specifies the type of model (see train Model List or train Models By Tag). To illustrate, we will fit a boosted tree model via the gbm package. The basic syntax for fitting this model using repeated cross-validation is shown below:
set.seed(825) gbmFit1 <- train(Class ~ ., data = training, method = "gbm", trControl = fitControl, ## This last option is actually one ## for gbm() that passes through verbose = FALSE) gbmFit1
Stochastic Gradient Boosting 157 samples 60 predictors 2 classes: 'M', 'R' No pre-processing Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: interaction.depth n.trees Accuracy Kappa Accuracy SD Kappa SD 1 50 0.8 0.5 0.1 0.2 1 100 0.8 0.6 0.1 0.2 1 200 0.8 0.6 0.09 0.2 2 50 0.8 0.6 0.1 0.2 2 100 0.8 0.6 0.09 0.2 2 200 0.8 0.6 0.1 0.2 3 50 0.8 0.6 0.09 0.2 3 100 0.8 0.6 0.09 0.2 3 200 0.8 0.6 0.08 0.2 Tuning parameter 'shrinkage' was held constant at a value of 0.1 Accuracy was used to select the optimal model using the largest value. The final values used for the model were n.trees = 150, interaction.depth = 3 and shrinkage = 0.1.
For a gradient boosting machine (GBM) model, there are three main tuning parameters:
- number of iterations, i.e. trees, (called n.trees in the gbm function)
- complexity of the tree, called interaction.depth
- learning rate: how quickly the algorithm adapts, called shrinkage
The default values tested for this model are shown in the first two
columns (shrinkage is not shown beause the grid set of
candidate models all use a value of 0.1 for this tuning parameter).
The column labeled "Accuracy" is the overall agreement rate
averaged over cross-validation iterations. The agreement standard
deviation is also calculated from the cross-validation results. The
column "Kappa" is Cohen's (unweighted) Kappa statistic
averaged across the resampling results. train works with
specific models (see train Model List
or train Models By Tag).
For these models, train can automatically
create a grid of tuning parameters. By default, if p is the number
of tuning parameters, the grid size is 3^p. As another example, regularized
discriminant analysis (RDA) models have two parameters
(gamma and lambda), both of which lie on [0,
1]. The default training grid would produce nine combinations in this
two-dimensional space.
There are several notes regarding specific model behaviors for train. There is additional functionality in train that is described in the next section.
Customizing the Tuning Process
There are a few ways to customize the process of selecting tuning/complexity parameters and building the final model.
Pre-Processing Options
As previously mentioned,train can pre-process the data in various ways prior to model fitting. The function preProcess is automatically used. This function can be used for centering and scaling, imputation (see details below), applying the spatial sign transformation and feature extraction via principal component analysis or independent component analysis.
To specify what pre-processing should occur, the train function has an argument called preProcess. This argument takes a character string of methods that would normally be passed to the method argument of the preProcess function. Additional options to the preProcess function can be passed via the trainControl function.
These processing steps would be applied during any predictions
generated using predict.train, extractPrediction or
extractProbs (see details later in this document). The
pre-processing would not be applied to predictions that
directly use the object$finalModel object.
For imputation, there are three methods currently implemented:
- k-nearest neighbors takes a sample with missing values and finds the k closest samples in the training set. The average of the k training set values for that predictor are used as a substitute for the original data. When calculating the distances to the training set samples, the predictors used in the calculation are the ones with no missing values for that sample and no missing values in the training set.
- another approach is to fit a bagged tree model for each predictor using the training set samples. This is usually a fairly accurate model and can handle missing values. When a predictor for a sample requires imputation, the values for the other predictors are fed through the bagged tree and the prediction is used as the new value. This model can have significant computational cost.
- the median of the predictor's training set values can be used to estimate the missing data.
If there are missing values in the training set, PCA and ICA models only use complete samples.
Alternate Tuning Grids
The tuning parameter grid can be specified by the user. The argument
tuneGrid can take a data frame with columns for each tuning parameter. The column names should be the same as the fitting function's arguments. For the previously mentioned RDA example, the names would be
gamma and lambda. train will tune the
model over each combination of values in the rows.
For the boosted tree model, we can fix the learning rate and evaluate more than three values of n.trees:
gbmGrid <- expand.grid(interaction.depth = c(1, 5, 9), n.trees = (1:30)*50, shrinkage = 0.1) nrow(gbmGrid) set.seed(825) gbmFit2 <- train(Class ~ ., data = training, method = "gbm", trControl = fitControl, verbose = FALSE, ## Now specify the exact models ## to evaludate: tuneGrid = gbmGrid) gbmFit2
Stochastic Gradient Boosting 157 samples 60 predictors 2 classes: 'M', 'R' No pre-processing Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: interaction.depth n.trees Accuracy Kappa Accuracy SD Kappa SD 1 50 0.77 0.53 0.1 0.2 1 100 0.78 0.56 0.095 0.19 1 150 0.79 0.58 0.094 0.19 1 200 0.79 0.58 0.094 0.19 : : : : : : 9 1200 0.82 0.64 0.092 0.19 9 1200 0.82 0.64 0.09 0.18 9 1300 0.83 0.65 0.088 0.18 9 1400 0.82 0.64 0.092 0.19 9 1400 0.82 0.63 0.095 0.19 9 1400 0.82 0.63 0.092 0.19 9 1500 0.82 0.63 0.093 0.19 Tuning parameter 'shrinkage' was held constant at a value of 0.1 Accuracy was used to select the optimal model using the largest value. The final values used for the model were n.trees = 1400, interaction.depth = 5 and shrinkage = 0.1.
Plotting the Resampling Profile
The plot function can be used to examine the relationship between the estimates of performance and the tuning parameters. For example, a simple invokation of the function shows the results for the first performance measure:
trellis.par.set(caretTheme()) plot(gbmFit2)
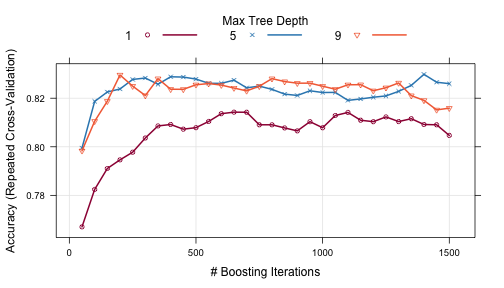
Other performance metrics can be shown using the metric option:
trellis.par.set(caretTheme()) plot(gbmFit2, metric = "Kappa")
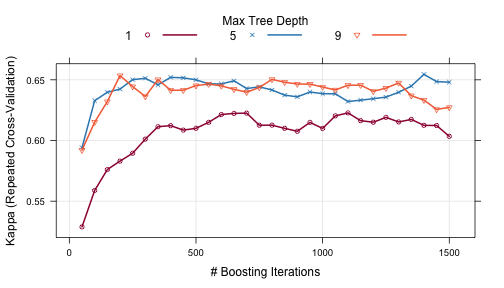
Other types of plot are also available. See ?plot.train for more details.
The code below shows a heatmap of the results:
trellis.par.set(caretTheme()) plot(gbmFit2, metric = "Kappa", plotType = "level", scales = list(x = list(rot = 90)))
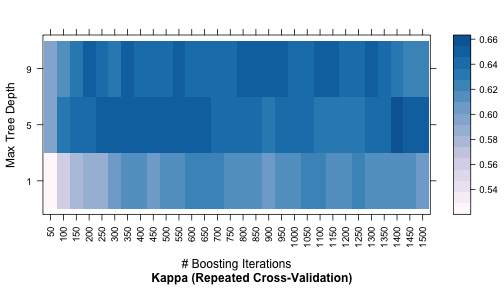
A ggplot method can also be used:
ggplot(gbmFit2)
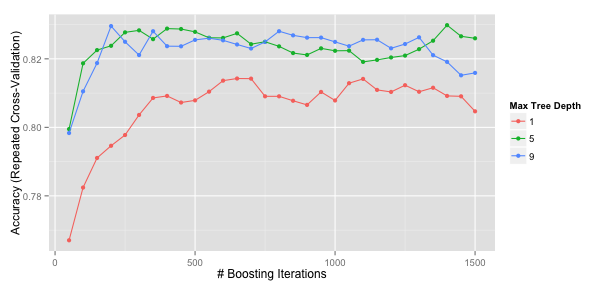
There are also plot functions that show more detailed representations of the
resampled estimates. See ?xyplot.train for more details.
From these plots, a different set of tuning parameters may be desired. To change the
final values without starting the whole process again, the update.train
can be used to refit the final model. See ?update.train
The trainControl Function
The function trainControl generates parameters that further control how models are created, with possible values:
- method: The resampling method: "boot", "cv", "LOOCV", "LGOCV", "repeatedcv", "timeslice", "none" and "oob". The last value, out-of-bag estimates, can only be used by random forest, bagged trees, bagged earth, bagged flexible discriminant analysis, or conditional tree forest models. GBM models are not included (the gbm package maintainer has indicated that it would not be a good idea to choose tuning parameter values based on the model OOB error estimates with boosted trees). Also, for leave-one-out cross-validation, no uncertainty estimates are given for the resampled performance measures.
- number and repeats: number controls with the number of folds in K-fold cross-validation or number of resampling iterations for bootstrapping and leave-group-out cross-validation. repeats applied only to repeated K-fold cross-validation. Suppose that method = "repeatedcv", number = 10 and repeats = 3,then three separate 10-fold cross-validations are used as the resampling scheme.
- verboseIter: A logical for printing a training log.
- returnData: A logical for saving the data into a slot
called
trainingData. - p: For leave-group out cross-validation: the training percentage
- For method = "timeslice", trainControl has options initialWindow, horizon and fixedWindow that govern how cross-validation can be used for time series data.
- classProbs: a logical value determining whether class probabilities should be computed for held-out samples during resample.
- index and indexOut: optional lists with elements for each resampling iteration. Each list element is the sample rows used for training at that iteration or should be held-out. When these values are not specified, train will generate them.
- summaryFunction: a function to compute alternate performance summaries.
- selectionFunction: a function to choose the optimal tuning parameters. and examples.
- PCAthresh, ICAcomp and k: these are all options to pass to the preProcess function (when used).
- returnResamp: a character string containing one of the following values: "all", "final" or "none". This specifies how much of the resampled performance measures to save.
- allowParallel: a logical that governs whether train should use parallel processing (if availible).
There are several other options not discussed here.
Alternate Performance Metrics
The user can change the metric used to determine the best settings. By default, RMSE and R2 are computed for regression while accuracy and Kappa are computed for classification. Also by default, the parameter values are chosen using RMSE and accuracy, respectively for regression and classification. The metric argument of the train function allows the user to control which the optimality criterion is used. For example, in problems where there are a low percentage of samples in one class, using metric = "Kappa" can improve quality of the final model.
If none of these parameters are satisfactory, the user can also compute custom performance metrics. The trainControl function has a argument called summaryFunction that specifies a function for computing performance. The function should have these arguments:
- data is a reference for a data frame or matrix with
columns called
obsandpredfor the observed and predicted outcome values (either numeric data for regression or character values for classification). Currently, class probabilities are not passed to the function. The values in data are the held-out predictions (and their associated reference values) for a single combination of tuning parameters. If the classProbs argument of the trainControl object is set to TRUE, additional columns indatawill be present that contains the class probabilities. The names of these columns are the same as the class levels. Also, if weights were specified in the call to train, a column calledweightswill also be in the data set. - lev is a character string that has the outcome factor levels taken from the training data. For regression, a value of NULL is passed into the function.
- model is a character string for the model being used (i.e. the value passed to the method argument of train).
The output to the function should be a vector of numeric summary metrics with non-null names. By default, train evaluate classification models in terms of the predicted classes. Optionally, class probabilities can also be used to measure performance. To obtain predicted class probabilities within the resampling process, the argument classProbs in trainControl must be set to TRUE. This merges columns of probabilities into the predictions generated from each resample (there is a column per class and the column names are the class names).
As shown in the last section, custom functions can be used to calculate performance scores that are averaged over the resamples. Another built-in function, twoClassSummary, will compute the sensitivity, specificity and area under the ROC curve:
head(twoClassSummary)
1 function (data, lev = NULL, model = NULL)
2 {
3 require(pROC)
4 if (!all(levels(data[, "pred"]) == levels(data[, "obs"])))
5 stop("levels of observed and predicted data do not match")
6 rocObject <- try(pROC::roc(data$obs, data[, lev[1]]), silent = TRUE)
To rebuild the boosted tree model using this criterion, we can see the relationship between the tuning parameters and the area under the ROC curve using the following code:
fitControl <- trainControl(method = "repeatedcv", number = 10, repeats = 10, ## Estimate class probabilities classProbs = TRUE, ## Evaluate performance using ## the following function summaryFunction = twoClassSummary) set.seed(825) gbmFit3 <- train(Class ~ ., data = training, method = "gbm", trControl = fitControl, verbose = FALSE, tuneGrid = gbmGrid, ## Specify which metric to optimize metric = "ROC") gbmFit3
Stochastic Gradient Boosting 157 samples 60 predictors 2 classes: 'M', 'R' No pre-processing Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: interaction.depth n.trees ROC Sens Spec ROC SD Sens SD Spec SD 1 50 0.86 0.83 0.69 0.1 0.15 0.17 1 100 0.87 0.84 0.73 0.093 0.14 0.16 1 150 0.88 0.85 0.74 0.088 0.13 0.17 1 200 0.88 0.86 0.75 0.084 0.14 0.17 : : : : : : : : 9 1200 0.91 0.89 0.76 0.075 0.12 0.16 9 1200 0.91 0.89 0.75 0.074 0.12 0.15 9 1300 0.91 0.89 0.75 0.075 0.11 0.15 9 1400 0.91 0.89 0.76 0.073 0.11 0.15 9 1400 0.91 0.88 0.76 0.073 0.12 0.15 9 1400 0.91 0.87 0.77 0.072 0.13 0.15 9 1500 0.92 0.87 0.78 0.072 0.13 0.15 Tuning parameter 'shrinkage' was held constant at a value of 0.1 ROC was used to select the optimal model using the largest value. The final values used for the model were n.trees = 1500, interaction.depth = 9 and shrinkage = 0.1.
In this case, the average area under the ROC curve associated with the optimal tuning parameters was 0.916 across the 100 resamples.
Choosing the Final Model
Another method for customizing the tuning process is to modify the algorithm that is used to select the "best" parameter values, given the performance numbers. By default, the train function chooses the model with the largest performance value (or smallest, for mean squared error in regression models). Other schemes for selecting model can be used. Breiman et al (1984) suggested the "one standard error rule" for simple tree-based models. In this case, the model with the best performance value is identified and, using resampling, we can estimate the standard error of performance. The final model used was the simplest model within one standard error of the (empirically) best model. With simple trees this makes sense, since these models will start to over-fit as they become more and more specific to the training data.
train allows the user to specify alternate rules for
selecting the final model. The argument selectionFunction
can be used to supply a function to algorithmically determine the
final model. There are three existing functions in the package:
best is chooses the largest/smallest value, oneSE
attempts to capture the spirit of Breiman et al (1984) and
tolerance selects the least complex model within some percent
tolerance of the best value. See ?best for more details.
User-defined functions can be used, as long as they have the following arguments:
- x is a data frame containing the tune parameters and their associated performance metrics. Each row corresponds to a different tuning parameter combination.
- metric a character string indicating which performance metric should be optimized (this is passed in directly from the metric argument of train.
- maximize is a single logical value indicating whether larger values of the performance metric are better (this is also directly passed from the call to train).
The function should output a single integer indicating which row in
x is chosen.
As an example, if we chose the previous boosted tree model on the basis of overall accuracy, we would choose: n.trees = 1500, interaction.depth = 9, shrinkage = 0.1. However, the scale in this plots is fairly tight, with accuracy values ranging from 0.863 to 0.916. A less complex model (e.g. fewer, more shallow trees) might also yield acceptable accuracy.
The tolerance function could be used to find a less complex model based on (x-xbest)/xbestx 100, which is the percent difference. For example, to select parameter values based on a 2% loss of performance:
whichTwoPct <- tolerance(gbmFit3$results, metric = "ROC", tol = 2, maximize = TRUE) cat("best model within 2 pct of best:\n")
best model within 2 pct of best:
gbmFit3$results[whichTwoPct, 1:6]
shrinkage interaction.depth n.trees ROC Sens Spec 32 0.1 5 100 0.8988 0.864 0.765
This indicates that we can get a less complex model with an area under the ROC curve of 0.899 (compared to the "pick the best" value of 0.916).
The main issue with these functions is related to ordering the models
from simplest to complex. In some cases, this is easy (e.g. simple
trees, partial least squares), but in cases such as this model, the ordering of
models is subjective. For example, is a boosted tree model using 100
iterations and a tree depth of 2 more complex than one with 50
iterations and a depth of 8? The package makes some choices regarding
the orderings. In the case of boosted trees, the package assumes that
increasing the number of iterations adds complexity at a faster rate
than increasing the tree depth, so models are ordered on the number of
iterations then ordered with depth. See ?best for more
examples for specific models.
Extracting Predictions and Class Probabilities
As previously mentioned, objects produced by the train
function contain the "optimized" model in the finalModel
sub-object. Predictions can be made from these objects as usual. In
some cases, such as pls or gbm objects, additional
parameters from the optimized fit may need to be specified. In these
cases, the train objects uses the results of the parameter
optimization to predict new samples. For example, if predictions were create
using predict.gbm, the user would have to specify the number of trees
directly (there is no default). Also, for binary classification, the predictions
from this function take the form of the probability of one of the classes, so
extra steps are required to convert this to a factor vector. predict.train
automatically handles these details for this (and for other models).
Also, there are very few standard syntaxes for model predictions in R. For example, to get class probabilities, many predict methods have an argument called type that is used to specify whether the classes or probabilities should be generated. Different packages use different values of type, such as "prob", "posterior", "response", "probability" or "raw". In other cases, completely different syntax is used.
For predict.train, the type options are standardized to be "class" and "prob" (the underlying code matches these to the appropriate choices for each model. For example:
predict(gbmFit3, newdata = head(testing))
[1] R R R R M M Levels: M R
predict(gbmFit3, newdata = head(testing), type = "prob")
M R 1 1.957e-06 0.9999980 2 4.824e-14 1.0000000 3 1.118e-32 1.0000000 4 1.528e-10 1.0000000 5 9.997e-01 0.0003027 6 9.995e-01 0.0004851
Exploring and Comparing Resampling Distributions
Within-Model
There are several lattice functions than can be used to explore relationships between tuning parameters and the resampling results for a specific model:
- xyplot and stripplot can be used to plot resampling statistics against (numeric) tuning parameters.
- histogram and densityplot can also be used to look at distributions of the tuning parameters across tuning parameters.
For example, the following statements create a density plot:
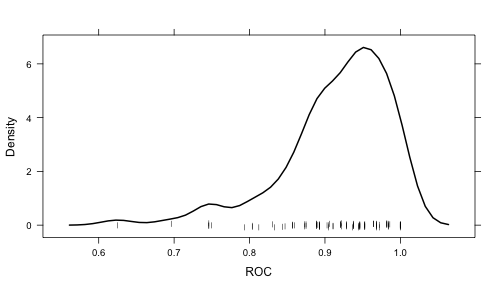
Note that if you are interested in plotting the resampling results across multiple tuning parameters, the option resamples = "all" should be used in the control object.
Between-Models
The caret package also includes functions to characterize the differences between models (generated using train, sbf or rfe) via their resampling distributions. These functions are based on the work of Hothorn et al. (2005) and Eugster et al (2008).
First, a support vector machine model is fit to the Sonar data. The data are centered and scaled using the preProc argument. Note that the same random number seed is set prior to the model that is idenditcal to the seed used for the boosted tree model. This ensures that the same resampling sets are used, which will come in handy when we compare the resamling profiles between models.
set.seed(825) svmFit <- train(Class ~ ., data = training, method = "svmRadial", trControl = fitControl, preProc = c("center", "scale"), tuneLength = 8, metric = "ROC") svmFit
Support Vector Machines with Radial Basis Function Kernel 157 samples 60 predictors 2 classes: 'M', 'R' Pre-processing: centered, scaled Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: C ROC Sens Spec ROC SD Sens SD Spec SD 0.2 0.9 0.7 0.7 0.08 0.1 0.2 0.5 0.9 0.8 0.8 0.06 0.1 0.2 1 0.9 0.9 0.8 0.06 0.1 0.1 2 0.9 0.9 0.8 0.05 0.1 0.2 4 0.9 0.9 0.8 0.05 0.1 0.2 8 0.9 0.9 0.8 0.05 0.1 0.2 20 0.9 0.9 0.8 0.06 0.09 0.2 30 0.9 0.9 0.8 0.06 0.1 0.2 Tuning parameter 'sigma' was held constant at a value of 0.01234 ROC was used to select the optimal model using the largest value. The final values used for the model were sigma = 0.01 and C = 8.
Also, a regularized discriminant analysis model was fit.
set.seed(825) rdaFit <- train(Class ~ ., data = training, method = "rda", trControl = fitControl, tuneLength = 4, metric = "ROC") rdaFit
Regularized Discriminant Analysis 157 samples 60 predictors 2 classes: 'M', 'R' No pre-processing Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: gamma lambda ROC Sens Spec ROC SD Sens SD Spec SD 0 0 0.8 0.8 0.8 0.1 0.1 0.2 0 0.3 0.8 0.8 0.8 0.1 0.1 0.2 0 0.7 0.8 0.8 0.8 0.1 0.1 0.2 0 1 0.9 0.8 0.8 0.1 0.1 0.2 0.3 0 0.9 0.9 0.8 0.07 0.1 0.2 0.3 0.3 0.9 0.9 0.8 0.08 0.1 0.1 0.3 0.7 0.9 0.9 0.8 0.07 0.1 0.2 0.3 1 0.9 0.9 0.8 0.08 0.1 0.2 0.7 0 0.9 0.9 0.7 0.08 0.1 0.2 0.7 0.3 0.9 0.9 0.7 0.09 0.1 0.2 0.7 0.7 0.9 0.9 0.7 0.09 0.1 0.2 0.7 1 0.9 0.9 0.7 0.09 0.1 0.2 1 0 0.7 0.7 0.6 0.1 0.2 0.2 1 0.3 0.7 0.7 0.6 0.1 0.2 0.2 1 0.7 0.7 0.7 0.6 0.1 0.2 0.2 1 1 0.7 0.7 0.7 0.1 0.2 0.2 ROC was used to select the optimal model using the largest value. The final values used for the model were gamma = 0.3 and lambda = 0.
Given these models, can we make statistical statements about their performance differences? To do this, we first collect the resampling results using resamples.
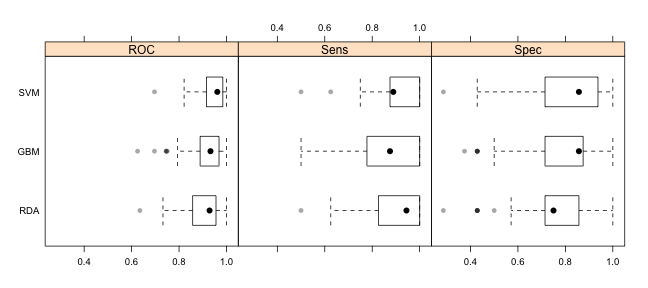
resamps <- resamples(list(GBM = gbmFit3, SVM = svmFit, RDA = rdaFit)) resamps
Call: resamples.default(x = list(GBM = gbmFit3, SVM = svmFit, RDA = rdaFit)) Models: GBM, SVM, RDA Number of resamples: 100 Performance metrics: ROC, Sens, Spec Time estimates for: everything, final model fit
summary(resamps)
Call:
summary.resamples(object = resamps)
Models: GBM, SVM, RDA
Number of resamples: 100
ROC
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
GBM 0.625 0.889 0.933 0.916 0.968 1 0
SVM 0.696 0.918 0.961 0.946 0.984 1 0
RDA 0.635 0.857 0.929 0.907 0.954 1 0
Sens
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
GBM 0.5 0.778 0.875 0.867 1 1 0
SVM 0.5 0.875 0.889 0.910 1 1 0
RDA 0.5 0.851 0.944 0.903 1 1 0
Spec
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
GBM 0.375 0.714 0.857 0.782 0.875 1 0
SVM 0.286 0.714 0.857 0.815 0.906 1 0
RDA 0.286 0.714 0.750 0.761 0.857 1 0
Note that, in this case, the option resamples = "final" should be used in the control objects.
There are several
trellis.par.set(theme1) bwplot(resamps, layout = c(3, 1))
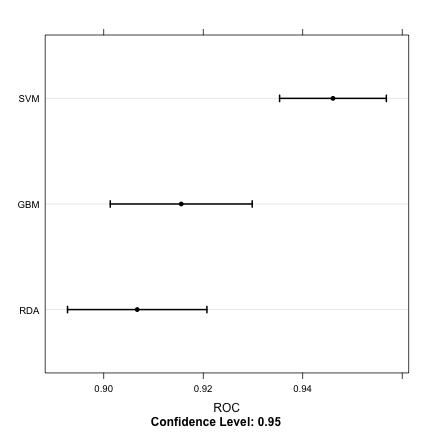
trellis.par.set(caretTheme()) dotplot(resamps, metric = "ROC")
trellis.par.set(theme1) xyplot(resamps, what = "BlandAltman")
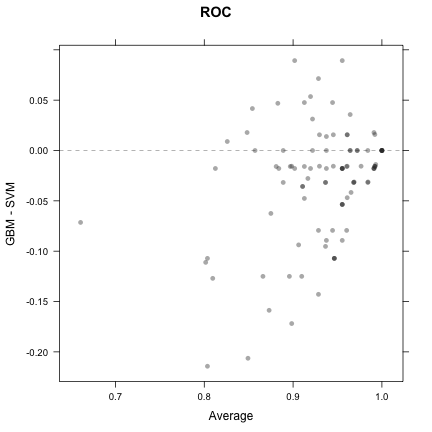
splom(resamps)
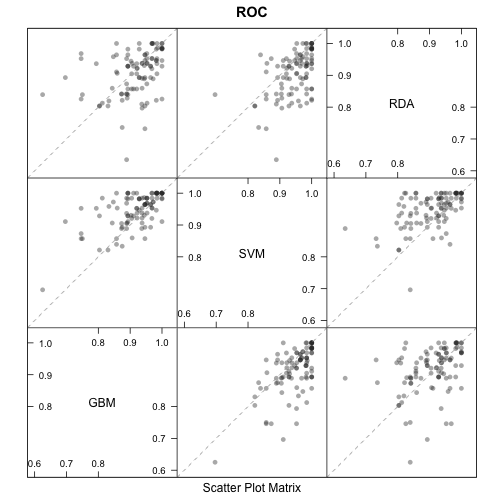
Other visualizations are availible in densityplot.resamples and parallel.resamples
Since models are fit on the same versions of the training data, it makes sense to make inferences on the differences between models. In this way we reduce the within-resample correlation that may exist. We can compute the differences, then use a simple t-test to evaluate the null hypothesis that there is no difference between models.
difValues <- diff(resamps) difValues
Call: diff.resamples(x = resamps) Models: GBM, SVM, RDA Metrics: ROC, Sens, Spec Number of differences: 3 p-value adjustment: bonferroni
summary(difValues)
Call:
summary.diff.resamples(object = difValues)
p-value adjustment: bonferroni
Upper diagonal: estimates of the difference
Lower diagonal: p-value for H0: difference = 0
ROC
GBM SVM RDA
GBM -0.03050 0.00885
SVM 1.81e-06 0.03935
RDA 0.824 5.02e-08
Sens
GBM SVM RDA
GBM -0.04333 -0.03611
SVM 0.000983 0.00722
RDA 0.042556 1.000000
Spec
GBM SVM RDA
GBM -0.0334 0.0211
SVM 0.05664 0.0545
RDA 0.71443 0.00414
trellis.par.set(theme1) bwplot(difValues, layout = c(3, 1))
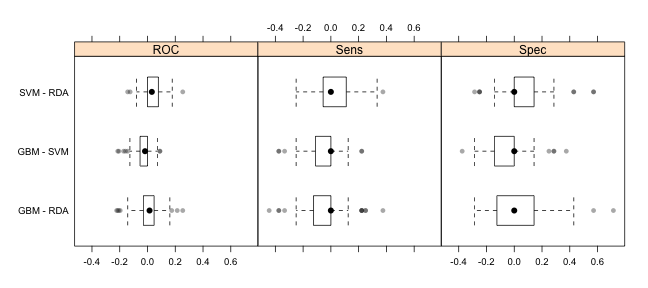
trellis.par.set(caretTheme()) dotplot(difValues)
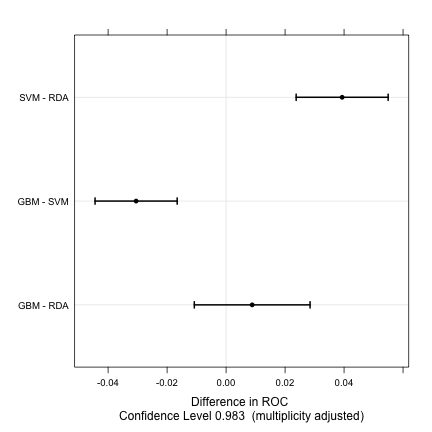
Fitting Models Without Parameter Tuning
In cases where the model tuning values are known, train can be used to fit the model to the entire training set without any resampling or parameter tuning. Using the method = "none" option in trainControl can be used. For example:
fitControl <- trainControl(method = "none", classProbs = TRUE) set.seed(825) gbmFit4 <- train(Class ~ ., data = training, method = "gbm", trControl = fitControl, verbose = FALSE, ## Only a single model can be passed to the ## function when no resampling is used: tuneGrid = data.frame(interaction.depth = 4, n.trees = 100, shrinkage = .1), metric = "ROC") gbmFit4
Stochastic Gradient Boosting 157 samples 60 predictors 2 classes: 'M', 'R' No pre-processing Resampling: None
Note that plot.train, resamples, confusionMatrix.train and several other functions will not work with this object but predict.train and others will:
predict(gbmFit4, newdata = head(testing))
[1] R R R R M M Levels: M R
predict(gbmFit4, newdata = head(testing), type = "prob")
M R 1 0.4060186 0.5940 2 0.0301124 0.9699 3 0.0009584 0.9990 4 0.0399826 0.9600 5 0.9614988 0.0385 6 0.7496510 0.2503