Contents
- Introduction
- Illustrative Example 1: SVMs with Laplacian Kernels
- Model Components
- Illustrative Example 2: Something More Complicated - LogitBoost
- Illustrative Example 3: SMOTE During Resampling
- Illustrative Example 4: PLS Feature Extraction Pre-Processing
- Illustrative Example 5: Optimizing probability thresholds for class imbalances
Introduction
The package contains a large number of predictive model interfaces. However, you may want to create your own because:
- you are testing out a novel model or the package doesn't have a model that you are interested in
- you would like to run an existing model in the package your own way
- there are pre-processing or sampling steps not contained in the package or you just don't like the way the package does things
You can still get the benefits of the caret infrastructure by creating your own model.
Currently, when you specify the type of model that you are interested in (e.g. type = "lda"), the train function runs another function called getModelInfo to retrieve the specifics of that model from the existing catalog. For example:
ldaModelInfo <- getModelInfo(model = "lda", regex = FALSE)[[1]] ## Model components names(ldaModelInfo)
[1] "label" "library" "loop" "type" "parameters" [6] "grid" "fit" "predict" "prob" "predictors" [11] "tags" "levels" "sort"
To use your own model, you can pass a list of these components to type. This page will describe those components in detail.
Illustrative Example 1: SVMs with Laplacian Kernels
The package currently contains support vector machine (SVM) models using linear, polynomial and radial basis function kernels. The kernlab package has other functions, including the Laplacian kernel. We will illustrate the model components for this model, which has two parameters: the standard cost parameter for SVMs and one kernel parameter (sigma)
Model Components
You can pass a list of information to the method argument in train. For models that are built-in to the package, you can just pass the method name as before.
There are some basic components of the list for custom models. A brief description is below for each then, after setting up and example, each will be described in detail. The list should have the following elements:
- library is a character vector of package names that will be needed to fit the model or calculate predictions. NULL can also be used.
- type is a simple character vector with values "Classification", "Regression" or both.
- parameters is a data frame with three simple attributes for each tuning parameter (if any): the argument name (e.g. mtry), the type of data in the parameter grid and textual labels for the parameter.
- grid is a function that is used to create the tuning grid (unless the user gives the exact values of the parameters via tuneGrid)
- fit is a function that fits the model
- predict is the function that creates predictions
- prob is a function that can be used to create class probabilities (if applicable)
- sort is a function that sorts the parameter from most complex to least
- loop is an optional function for advanced users for models that can create multiple submodel predictions from the same object.
- levels is an optional function, primarily for classification models using S4 methods to return the factor levels of the outcome.
- tags is an optional character vector that has subjects associated with the model, such as Tree-Based Model or Embedded Feature Selection. This string is used by the package to create additional documentation pages on the package website.
- label is an optional character string that names the model (e.g. "Linear Discriminant Analysis").
- predictors is an optional function that returns a character vector that contains the names of the predictors that we used in the prediction equation.
- varImp is an optional function that calculates variable importance metrics for the model (if any).
In the caret package, the subdirectory models has all the code for each model that train interfaces with and these can be used as prototypes for your model.
Let's create a new model for a classification support vector machine using the Laplacian kernel function. We will use the kernlab package's ksvm function. The kernel has two parameters: the standard cost parameter for SVMs and one kernel parameter (sigma).
To start, we'll create a new list:
lpSVM <- list(type = "Classification", library = "kernlab", loop = NULL)
This model can also be used for regression but we will constrain things here for simplicity. For other SVM models, the type value would be c("Classification", "Regression").
The library value checks to see if this package is installed and loads it whenever it is needed (e.g. before modeling or prediction).
The parameters Element
We have to create some basic information for the parameters in the form of a data frame. The first column is the name of the parameter. The convention is to use the argument name in the model function (e.g. the ksvm function here). Those values are C and sigma. Each is a number and we can give them labels of "Cost" and "Sigma", respectively. The parameters element would then be:
prm <- data.frame(parameter = c("C", "sigma"), class = rep("numeric", 2), label = c("Cost", "Sigma"))
Now we assign it to the model list:
lpSVM$parameters <- prm
Values of type can indicate numeric, character or logical data types.
The grid Element
This should be a function that takes parameters: x and y (for the predictors and outcome data) as well as len. The latter is the value of tuneLength that is potentially passed in through train.
The output should be a data frame of tuning parameter combinations with a column for each parameter. The column names should be the parameter name (e.g. the values of prm$parameter). In our case, let's vary the cost parameter on the log 2 scale. For the sigma parameter, we can use the kernlab function sigest to pre-estimate the value. Following ksvm we take the average of the low and high estimates. Here is a function we could use:
svmGrid <- function(x, y, len = NULL) { library(kernlab) ## This produces low, middle and high values for sigma ## (i.e. a vector with 3 elements). sigmas <- sigest(as.matrix(x), na.action = na.omit, scaled = TRUE) expand.grid(sigma = mean(sigmas[-2]), C = 2 ^((1:len) - 3)) }
Again, the user can pass their own grid via train's tuneGrid option or they can use this code to create a default grid.
We assign this function to the overall model list:
lpSVM$grid <- svmGrid
The fit Element
Here is where we fit the model. This fit function has several arguments:
- x, y: the current data used to fit the model
- wts: optional instance weights (not applicable for this particular model)
- param: the current tuning parameter values
- lev: the class levels of the outcome (or NULL in regression)
- last: a logical for whether the current fit is the final fit
- weights
- classProbs: a logical for whether class probabilities should be computed.
Here is something we could use for this model:
svmFit <- function(x, y, wts, param, lev, last, weights, classProbs, ...) { ksvm(x = as.matrix(x), y = y, kernel = rbfdot, kpar = list(sigma = param$sigma), C = param$C, prob.model = classProbs, ...) } lpSVM$fit <- svmFit
A few notes about this:
- Notice that the package is not loaded in the code. It is loaded prior to this function being called so it won't hurt if you load it again (but that's not needed).
- The ksvm function requires a matrix or predictors. If the original data were a data frame, this would throw and error.
- The tuning parameters are references in the param data frame. There is always a single row in this data frame.
- The probability model is fit based on the value of classProbs. This value is determined by the value given in trainControl.
- The three dots allow the user to pass options in from train to, in this case, the ksvm function. For example, if the user wanted to set the cache size for the function, they could list cache = 80 and this argument will be pass from train to ksvm.
- Any pre-processing that was requested in the call to train have been done. For example, if preProc = "center" was originally requested, the columns of x seen within this function are mean centered.
The predict Element
This is a function that produces a vector or predictions. In our case, these are class predictions but they could be numbers for regression models.
The arguments are:
- modelFit: the model produced by the fit code shown above.
- newdata: the predictor values of the instances being predicted (e.g. out-of-bag samples)
- preProc
- submodels: this an optional list of tuning parameters only used with the loop element discussed below. In most cases, it will be NULL.
Our function will be very simple:
svmPred <- function(modelFit, newdata, preProc = NULL, submodels = NULL) predict(modelFit, newdata) lpSVM$predict <- svmPred
The function predict.ksvm will automatically create a factor vector as output. The function could also produce character values. Either way, the innards of train will make them factors and ensure that the same levels as the original data are used.
The prob Element
If a regression model is being used or if the classification model does not create class probabilities a value of NULL can be used here instead of a function. Otherwise, the function arguments are the same as the pred function. The output should be a matrix or data frame of class probabilities with a column for each class. The column names should be the class levels.
We can use:
svmProb <- function(modelFit, newdata, preProc = NULL, submodels = NULL) predict(modelFit, newdata, type="probabilities") lpSVM$prob <- svmProb
If you look at some of the SVM examples in the models directory, the real functions used by train are much more complicated so that they can deal with model failures, probabilities that do not sum to 1 etc.
The sort Element
This is an optional function that sorts the tuning parameters from the simplest model to the most complex. There are times where this ordering is not obvious. This information is used when the performance values are tied across multiple parameters. We would probably want to choose the least complex model in those cases.
Here, we will sort by the cost value. Smaller values of C produce smoother class boundaries than larger values:
svmSort <- function(x) x[order(x$C), ] lpSVM$sort <- svmSort
The levels Element
train ensures that classification models always predict factors with the same levels. To do this at prediction time, the package needs to know the levels from the model object (specifically, the finalModels slot of the train object).
For model functions using S3 methods, train automatically attaches a character vector called obsLevels to the object and the package code uses this value. However, this strategy does not work for S4 methods. In these cases, the package will use the code found in the levels slot of the model list.
For example, the ksvm function uses S4 methods but, unlike most model functions, has a built--in function called lev that will extract the class levels (if any). In this case, our levels code would be:
lpSVM$levels <- function(x) lev(x)
In most other cases, the levels will beed to be extracted from data contained in the fitted model object. As another example, objects created using the ctree function in the party package would need to use:
function(x) levels(x@data@get("response")[, 1])
Again, this slot is only used for classification models using S4 methods.
We should now be ready to fit our model.
library(mlbench) data(Sonar) library(caret) set.seed(998) inTraining <- createDataPartition(Sonar$Class, p = .75, list = FALSE) training <- Sonar[ inTraining,] testing <- Sonar[-inTraining,] fitControl <- trainControl(method = "repeatedcv", ## 10-fold CV... number = 10, ## repeated ten times repeats = 10) set.seed(825) Laplacian <- train(Class ~ ., data = training, method = lpSVM, preProc = c("center", "scale"), tuneLength = 8, trControl = fitControl) print(Laplacian, digits = 3)
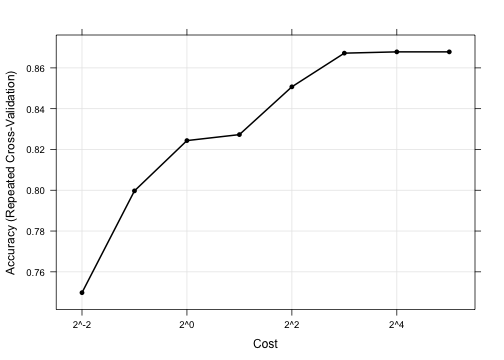
157 samples 60 predictors 2 classes: 'M', 'R' Pre-processing: centered, scaled Resampling: Cross-Validated (10 fold, repeated 10 times) Summary of sample sizes: 142, 142, 140, 142, 142, 141, ... Resampling results across tuning parameters: C Accuracy Kappa Accuracy SD Kappa SD 0.25 0.75 0.483 0.0909 0.191 0.5 0.8 0.589 0.0848 0.175 1 0.824 0.642 0.0846 0.172 2 0.827 0.648 0.0895 0.182 4 0.851 0.697 0.081 0.165 8 0.867 0.73 0.0829 0.17 16 0.868 0.731 0.0817 0.168 32 0.868 0.731 0.0817 0.168 Tuning parameter 'sigma' was held constant at a value of 0.01234 Accuracy was used to select the optimal model using the largest value. The final values used for the model were C = 16 and sigma = 0.0123.
A plot of the data shows that the model doesn't change when the cost value is above 16.
trellis.par.set(caretTheme()) plot(Laplacian, scales = list(x = list(log = 2)))
Illustrative Example 2: Something More Complicated - LogitBoost
The loop Element
This function can be used to create custom loops for models to tune over. In most cases, the function can just return the existing tuning grid.
For example, a LogitBoost model can be trained over the number of boosting iterations. In the caTools package, the LogitBoost function can be used to fit this model. For example:
mod <- LogitBoost(as.matrix(x), y, nIter = 51)
If we were to tune the model evaluating models where the number of iterations was 11, 21, 31, 41 and 51, the grid could be
lbGrid <- data.frame(nIter = seq(11, 51, by = 10))
During resampling, train could loop over all five rows in lbGrid and fit five models. However, the predict.LogitBoost function has an argument called nIter that can produce, in this case, predictions from mod for all five models.
Instead of train fitting five models, we could fit a single model with nIter = 51 and derive predictions for all five models using only mod.
The terminology used here is that nIter is a sequential tuning parameter (and the other parameters would be considered fixed).
The loop argument for models is used to produce two objects:
-
loop: this is the actual loop that is used by `train`. -
submodelsis a list that has as many elements as there are rows inloop. The list has all the "extra" parameter settings that can be derived for each model.
Going back to the LogitBoost example, we could have:
loop <- data.frame(.nIter = 51) loop
.nIter 1 51
submodels <- list(data.frame(nIter = seq(11, 41, by = 10))) submodels
[[1]] nIter 1 11 2 21 3 31 4 41
For this case, train first fits the nIter = 50 model. When the model is predicted, that code has a for loop that iterates over the elements of submodel[[1]] to get the predictions for the other 4 models.
In the end, predictions for all five models (for nIter = seq(11, 51, by = 10)) with a single model fit.
There are other models built-in to caret that are used this way. There are a number of models that have multiple sequential tuning parameters.
If the loop argument is left NULL the results of tuneGrid are used as the simple loop and is recommended for most situations. Note that the machinery that is used to "derive" the extra predictions is up to the user to create, typically in the predict and prob elements of the custom model object.
For the LogitBoost model, some simple code to create these objects would be:
fullGrid <- data.frame(nIter = seq(11, 51, by = 10)) ## Get the largest value of nIter to fit the 'full' model loop <- fullGrid[which.max(fullGrid$nIter), , drop = FALSE] loop
nIter 5 51
submodels <- fullGrid[-which.max(fullGrid$nIter), , drop = FALSE] ## This needs to be encased in a list in case there are more than one tuning ## parameter submodels <- list(submodels) submodels
[[1]] nIter 1 11 2 21 3 31 4 41
For the LogitBoost custom model object, we could use this code in the predict slot:
lbPred <- function(modelFit, newdata, preProc = NULL, submodels = NULL) { ## This model was fit with the maximum value of nIter out <- caTools::predict.LogitBoost(modelFit, newdata, type="class") ## In this case, 'submodels' is a data frame with the other values of ## nIter. We loop over these to get the other predictions. if(!is.null(submodels)) { ## Save _all_ the predictions in a list tmp <- out out <- vector(mode = "list", length = nrow(submodels) + 1) out[[1]] <- tmp for(j in seq(along = submodels$nIter)) { out[[j+1]] <- caTools::predict.LogitBoost(modelFit, newdata, nIter = submodels$nIter[j]) } } out }
A few more notes:
- The code in the fit element does not have to change.
- The prob slot works in the same way. The only difference is that the values saved in the outgoing lists are matrices or data frames of probabilities for each class.
-
After model training (i.e. predicting new samples), the value of submodels is set to
NULLand the code produces a single set of predictions. -
If the model had one sequential parameter and one fixed parameter, the
loopdata frame would have two columns (one for each parameter). If the model is tuned over more than one value of the fixed parameter, thesubmodelslist would have more than one element. Ifloophad 10 rows, then length(submodels) would be 10 and loop[i,] would be linked to submodels[[i]].
Here is a slimmed down version of the logitBoost code already in the package:
lbFuncs <- list(library = "caTools", loop = function(grid) { loop <- grid[which.max(grid$nIter),,drop = FALSE] submodels <- grid[-which.max(grid$nIter),,drop = FALSE] submodels <- list(submodels) list(loop = loop, submodels = submodels) }, type = "Classification", parameters = data.frame(parameter = 'nIter', class = 'numeric', label = '# Boosting Iterations'), grid = function(x, y, len = NULL) data.frame(nIter = 1 + ((1:len)*10)), fit = function(x, y, wts, param, lev, last, weights, classProbs, ...) { LogitBoost(as.matrix(x), y, nIter = param$nIter) }, predict = function(modelFit, newdata, preProc = NULL, submodels = NULL) { out <- predict(modelFit, newdata, type="class") if(!is.null(submodels)) { tmp <- out out <- vector(mode = "list", length = nrow(submodels) + 1) out[[1]] <- tmp for(j in seq(along = submodels$nIter)) { out[[j+1]] <- predict(modelFit, newdata, nIter = submodels$nIter[j]) } } out }, prob = NULL, sort = function(x) x)
Should you care about this? Let's tune the model over the same data set used for the SVM model above and see how long it takes:
set.seed(825) lb1 <- system.time(train(Class ~ ., data = training, method = lbFuncs, tuneLength = 3, trControl = fitControl)) lb1
user system elapsed 27.314 1.489 4.946
## Now get rid of the submodel parts lbFuncs2 <- lbFuncs lbFuncs2$predict = function(modelFit, newdata, preProc = NULL, submodels = NULL) predict(modelFit, newdata, type="class") lbFuncs2$loop <- NULL set.seed(825) lb2 <- system.time(train(Class ~ ., data = training, method = lbFuncs2, tuneLength = 3, trControl = fitControl)) lb2
user system elapsed 16.004 1.321 11.295
On a data set with 157 instances and 60 predictors and a model that is tuned over only 3 parameter values, there is a 2.28-fold speed-up. If the model were more computationally taxing or the data set were larger or the number of tune parameters that were evaluated was larger, the speed-up would increase. Here is a plot of the speed-up for a few more values of tuneLength:
bigGrid <- data.frame(nIter = seq(1, 151, by = 10)) results <- bigGrid results$SpeedUp <- NA for(i in 2:nrow(bigGrid)){ rm(lb1, lb2) set.seed(825) lb1 <- system.time(train(Class ~ ., data = training, method = lbFuncs, tuneGrid = bigGrid[1:i,,drop = FALSE], trControl = fitControl)) set.seed(825) lb2 <- system.time(train(Class ~ ., data = training, method = lbFuncs2, tuneGrid = bigGrid[1:i,,drop = FALSE], trControl = fitControl)) results$SpeedUp[i] <- lb2[3]/lb1[3] } trellis.par.set(caretTheme()) xyplot(SpeedUp ~ nIter, data = results, xlab = "LogitBoost Iterations", ylab = "Speed-Up", type = c("p", "g", "r"))
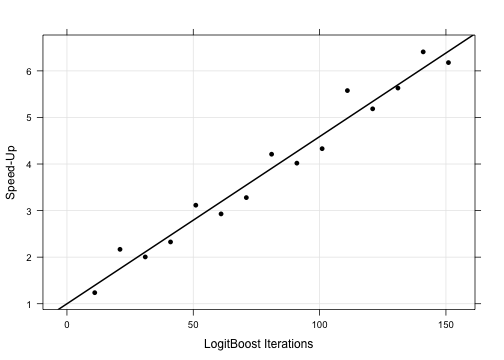
The speed-ups show a significant decrease in training time using this method.
Illustrative Example 3: SMOTE During Resampling
Other example is related to class imbalances. It might be helpful to sample the data so that the classes have a more balanced frequency distribution in the training set. One way to do this is the SMOTE algorithm where the majority class is down-sampled while new instances are imputed in the minority class. To get a good sense of what the performance will be using cross-validation, we should run SMOTE within each resample (instead of once prior to the model training).
To do this, we will only modify the fit function. Suppose we want to fit an LDA model. First, we get the functions, then modify them:
ldaInfo <- getModelInfo("lda", regex = FALSE)[[1]] ldaInfo$fit
function(x, y, wts, param, lev, last, classProbs, ...) lda(x, y, ...)
ldaInfo$fit <- function(x, y, wts, param, lev, last, classProbs, ...) { library(DMwR) tmp <- as.data.frame(x) tmp$Class <- y smoted <- SMOTE(Class ~ ., data = tmp) lda(smoted[, names(smoted) != "Class"], smoted$Class, ...) }
We can simulate some data with a class imbalance and test this model and the usual LDA model.
set.seed(1135) imbal_train <- twoClassSim(n = 300, intercept = -17) imbal_test <- twoClassSim(n = 2000, intercept = -17) table(imbal_train$Class)
Class1 Class2 270 30
ldaCtrl <- trainControl(method = "repeatedcv", repeats = 10, classProbs = TRUE, summaryFunction = twoClassSummary) set.seed(346) ldaFit <- train(Class ~ ., data = imbal_train, method = "lda", metric = "ROC", trControl = ldaCtrl) set.seed(346) ldaDSFit <- train(Class ~ ., data = imbal_train, method = ldaInfo, metric = "ROC", trControl = ldaCtrl) ldaProb1 <- predict(ldaFit, imbal_test, type = "prob")[,1] ldaProb2 <- predict(ldaDSFit, imbal_test, type = "prob")[,1] roc(imbal_test$Class, ldaProb1, levels = rev(levels(imbal_test$Class)))
Call: roc.default(response = imbal_test$Class, predictor = ldaProb1, levels = rev(levels(imbal_test$Class))) Data: ldaProb1 in 142 controls (imbal_test$Class Class2) < 1858 cases (imbal_test$Class Class1). Area under the curve: 0.765
roc(imbal_test$Class, ldaProb2, levels = rev(levels(imbal_test$Class)))
Call: roc.default(response = imbal_test$Class, predictor = ldaProb2, levels = rev(levels(imbal_test$Class))) Data: ldaProb2 in 142 controls (imbal_test$Class Class2) < 1858 cases (imbal_test$Class Class1). Area under the curve: 0.744
For these data, SMOTE didn't seem to make much of a difference.
Illustrative Example 4: PLS Feature Extraction Pre-Processing
PCA is a common tool for feature extraction prior to modeling but is unsupervised. Partial Least Squares (PLS) is essentially a supervised version of PCA. For some data sets, there may be some benefit to using PLS to generate new features from the original data (the PLS scores) then use those as an input into a different predictive model. PLS requires parameter tuning. In the example below, we use PLS on a data set with highly correlated predictors then use the PLS scores in a random forest model.
The "trick" here is to save the PLS loadings along with the random forest model fit so that the loadings can be used on future samples for prediction. Also, the PLS and random forest models are jointly tuned instead of an initial modeling process that finalizes the PLS model, then builds the random forest model separately. In this was we optimize both at once. Another important point is that the resampling results reflect the variability in the random forest and PLS models. If we did PLS up-front then resampled the random forest model, we would under-estimate the noise in the modeling process.
The tecator spectroscopy data are used:
data(tecator) set.seed(930) ## We will model the protein content data trainMeats <- createDataPartition(endpoints[,3], p = 3/4) absorpTrain <- absorp[trainMeats[[1]], ] proteinTrain <- endpoints[trainMeats[[1]], 3] absorpTest <- absorp[-trainMeats[[1]], ] proteinTest <- endpoints[-trainMeats[[1]], 3]
Here is the model code:
pls_rf <- list(label = "PLS-RF", library = c("pls", "randomForest"), type = "Regression", ## Tune over both parameters at the same time parameters = data.frame(parameter = c('ncomp', 'mtry'), class = c("numeric", 'numeric'), label = c('#Components', '#Randomly Selected Predictors')), grid = function(x, y, len = NULL) { grid <- expand.grid(ncomp = seq(1, min(ncol(x) - 1, len), by = 1), mtry = 1:len) ## We can't have mtry > ncomp grid <- subset(grid, mtry <= ncomp) }, loop = NULL, fit = function(x, y, wts, param, lev, last, classProbs, ...) { ## First fit the pls model, generate the training set scores, ## then attach what is needed to the random forest object to ## be used later ## plsr only has a formula interface so create one data frame dat <- x dat$y <- y pre <- plsr(y~ ., data = dat, ncomp = param$ncomp) scores <- predict(pre, x, type = "scores") colnames(scores) <- paste("score", 1:param$ncomp, sep = "") mod <- randomForest(scores, y, mtry = param$mtry, ...) mod$projection <- pre$projection mod }, predict = function(modelFit, newdata, submodels = NULL) { ## Now apply the same scaling to the new samples scores <- as.matrix(newdata) %*% modelFit$projection colnames(scores) <- paste("score", 1:ncol(scores), sep = "") ## Predict the random forest model predict(modelFit, scores) }, prob = NULL, varImp = NULL, predictors = function(x, ...) rownames(x$projection), levels = function(x) x$obsLevels, sort = function(x) x[order(x[,1]),])
We fit the models and look at the resampling results for the joint model:
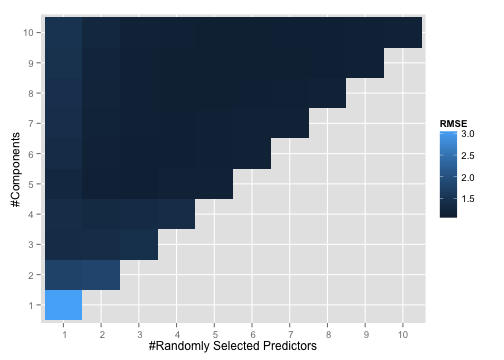
meatCtrl <- trainControl(method = "repeatedcv", repeats = 5) ## These will take a while for these data set.seed(184) plsrf <- train(absorpTrain, proteinTrain, method = pls_rf, preProc = c("center", "scale"), tuneLength = 10, ntree = 1000, trControl = meatCtrl) ggplot(plsrf, plotType = "level")
## How does random forest do on its own? set.seed(184) rfOnly <- train(absorpTrain, proteinTrain, method = "rf", tuneLength = 10, ntree = 1000, trControl = meatCtrl) getTrainPerf(rfOnly)
TrainRMSE TrainRsquared method 1 2.186 0.4953 rf
## How does random forest do on its own? set.seed(184) plsOnly <- train(absorpTrain, proteinTrain, method = "pls", tuneLength = 20, preProc = c("center", "scale"), trControl = meatCtrl) getTrainPerf(plsOnly)
TrainRMSE TrainRsquared method 1 0.629 0.9597 pls
The test set results indicate that these data like the linear model more than anything:
postResample(predict(plsrf, absorpTest), proteinTest)
RMSE Rsquared 1.3801 0.8126
postResample(predict(rfOnly, absorpTest), proteinTest)
RMSE Rsquared 2.0236 0.5786
postResample(predict(plsOnly, absorpTest), proteinTest)
RMSE Rsquared 0.7180 0.9438
Illustrative Example 5: Optimizing probability thresholds for class imbalances
This description was originally posted on this blog.
One of the toughest problems in predictive model occurs when the classes have a severe imbalance. In our book, we spend an entire chapter on this subject itself. One consequence of this is that the performance is generally very biased against the class with the smallest frequencies. For example, if the data have a majority of samples belonging to the first class and very few in the second class, most predictive models will maximize accuracy by predicting everything to be the first class. As a result there's usually great sensitivity but poor specificity. As a demonstration will use a simulation system described here. By default it has about a 50-50 class frequency but we can change this by altering the function argument called intercept:
library(caret) set.seed(442) trainingSet <- twoClassSim(n = 500, intercept = -16) testingSet <- twoClassSim(n = 500, intercept = -16) ## Class frequencies table(trainingSet$Class)
Class1 Class2 450 50
There is almost a 9:1 imbalance in these data. Let's use a standard random forest model with these data using the default value of mtry. We'll also use repeated 10-fold cross validation to get a sense of performance:
set.seed(949) mod0 <- train(Class ~ ., data = trainingSet, method = "rf", metric = "ROC", tuneGrid = data.frame(mtry = 3), ntree = 1000, trControl = trainControl(method = "repeatedcv", repeats = 5, classProbs = TRUE, summaryFunction = twoClassSummary)) getTrainPerf(mod0)
TrainROC TrainSens TrainSpec method 1 0.9577 0.9982 0.34 rf
## Get the ROC curve roc0 <- roc(testingSet$Class, predict(mod0, testingSet, type = "prob")[,1], levels = rev(levels(testingSet$Class))) roc0
Call: roc.default(response = testingSet$Class, predictor = predict(mod0, testingSet, type = "prob")[, 1], levels = rev(levels(testingSet$Class))) Data: predict(mod0, testingSet, type = "prob")[, 1] in 34 controls (testingSet$Class Class2) < 466 cases (testingSet$Class Class1). Area under the curve: 0.928
## Now plot plot(roc0, print.thres = c(.5), type = "S", print.thres.pattern = "%.3f (Spec = %.2f, Sens = %.2f)", print.thres.cex = .8, legacy.axes = TRUE)

Call: roc.default(response = testingSet$Class, predictor = predict(mod0, testingSet, type = "prob")[, 1], levels = rev(levels(testingSet$Class))) Data: predict(mod0, testingSet, type = "prob")[, 1] in 34 controls (testingSet$Class Class2) < 466 cases (testingSet$Class Class1). Area under the curve: 0.928
The area under the ROC curve is very high, indicating that the model has very good predictive power for these data. The plot shows the default probability cut off value of 50%. The sensitivity and specificity values associated with this point indicate that performance is not that good when an actual call needs to be made on a sample.
One of the most common ways to deal with this is to determine an alternate probability cut off using the ROC curve. But to do this well, another set of data (not the test set) is needed to set the cut off and the test set is used to validate it. We don't have a lot of data this is difficult since we will be spending some of our data just to get a single cut off value.
Alternatively the model can be tuned, using resampling, to determine any model tuning parameters as well as an appropriate cut off for the probabilities.
Suppose the model has one tuning parameter and we want to look at four candidate values for tuning. Suppose we also want to tune the probability cut off over 20 different thresholds. Now we have to look at 20×4=80 different models (and that is for each resample). One other feature that has been opened up his ability to use sequential parameters: these are tuning parameters that don't require a completely new model fit to produce predictions. In this case, we can fit one random forest model and get it's predicted class probabilities and evaluate the candidate probability cutoffs using these same hold-out samples. Here is what the model code looks like:
## Get the model code for the original random forest method: thresh_code <- getModelInfo("rf", regex = FALSE)[[1]] thresh_code$type <- c("Classification") ## Add the threshold as another tuning parameter thresh_code$parameters <- data.frame(parameter = c("mtry", "threshold"), class = c("numeric", "numeric"), label = c("#Randomly Selected Predictors", "Probability Cutoff")) ## The default tuning grid code: thresh_code$grid <- function(x, y, len = NULL) { p <- ncol(x) expand.grid(mtry = floor(sqrt(p)), threshold = seq(.01, .99, length = len)) } ## Here we fit a single random forest model (with a fixed mtry) ## and loop over the threshold values to get predictions from the same ## randomForest model. thresh_code$loop = function(grid) { library(plyr) loop <- ddply(grid, c("mtry"), function(x) c(threshold = max(x$threshold))) submodels <- vector(mode = "list", length = nrow(loop)) for(i in seq(along = loop$threshold)) { index <- which(grid$mtry == loop$mtry[i]) cuts <- grid[index, "threshold"] submodels[[i]] <- data.frame(threshold = cuts[cuts != loop$threshold[i]]) } list(loop = loop, submodels = submodels) } ## Fit the model independent of the threshold parameter thresh_code$fit = function(x, y, wts, param, lev, last, classProbs, ...) { if(length(levels(y)) != 2) stop("This works only for 2-class problems") randomForest(x, y, mtry = param$mtry, ...) } ## Now get a probability prediction and use different thresholds to ## get the predicted class thresh_code$predict = function(modelFit, newdata, submodels = NULL) { class1Prob <- predict(modelFit, newdata, type = "prob")[, modelFit$obsLevels[1]] ## Raise the threshold for class #1 and a higher level of ## evidence is needed to call it class 1 so it should ## decrease sensitivity and increase specificity out <- ifelse(class1Prob >= modelFit$tuneValue$threshold, modelFit$obsLevels[1], modelFit$obsLevels[2]) if(!is.null(submodels)) { tmp2 <- out out <- vector(mode = "list", length = length(submodels$threshold)) out[[1]] <- tmp2 for(i in seq(along = submodels$threshold)) { out[[i+1]] <- ifelse(class1Prob >= submodels$threshold[[i]], modelFit$obsLevels[1], modelFit$obsLevels[2]) } } out } ## The probabilities are always the same but we have to create ## mulitple versions of the probs to evaluate the data across ## thresholds thresh_code$prob = function(modelFit, newdata, submodels = NULL) { out <- as.data.frame(predict(modelFit, newdata, type = "prob")) if(!is.null(submodels)) { probs <- out out <- vector(mode = "list", length = length(submodels$threshold)+1) out <- lapply(out, function(x) probs) } out }
Basically, we define a list of model components (such as the fitting code, the prediction code, etc.) and feed this into the train function instead of using a pre-listed model string (such as method = "rf"). For this model and these data, there was an 8% increase in training time to evaluate 20 additional values of the probability cut off.
How do we optimize this model? Normally we might look at the area under the ROC curve as a metric to choose our final values. In this case the ROC curve is independent of the probability threshold so we have to use something else. A common technique to evaluate a candidate threshold is see how close it is to the perfect model where sensitivity and specificity are one. Our code will use the distance between the current model's performance and the best possible performance and then have train minimize this distance when choosing it's parameters. Here is the code that we use to calculate this:
fourStats <- function (data, lev = levels(data$obs), model = NULL) { ## This code will get use the area under the ROC curve and the ## sensitivity and specificity values using the current candidate ## value of the probability threshold. out <- c(twoClassSummary(data, lev = levels(data$obs), model = NULL)) ## The best possible model has sensitivity of 1 and specificity of 1. ## How far are we from that value? coords <- matrix(c(1, 1, out["Spec"], out["Sens"]), ncol = 2, byrow = TRUE) colnames(coords) <- c("Spec", "Sens") rownames(coords) <- c("Best", "Current") c(out, Dist = dist(coords)[1]) } set.seed(949) mod1 <- train(Class ~ ., data = trainingSet, method = thresh_code, ## Minimize the distance to the perfect model metric = "Dist", maximize = FALSE, tuneLength = 20, ntree = 1000, trControl = trainControl(method = "repeatedcv", repeats = 5, classProbs = TRUE, summaryFunction = fourStats)) mod1
Random Forest 500 samples 15 predictors 2 classes: 'Class1', 'Class2' No pre-processing Resampling: Cross-Validated (10 fold, repeated 5 times) Summary of sample sizes: 450, 450, 450, 450, 450, 450, ... Resampling results across tuning parameters: threshold ROC Sens Spec Dist ROC SD Sens SD Spec SD Dist SD 0.01 0.958 1 0 1 0.0349 0 0 0 0.0616 0.958 1 0 1 0.0349 0 0 0 0.113 0.958 1 0 1 0.0349 0 0 0 0.165 0.958 1 0 1 0.0349 0 0 0 0.216 0.958 1 0 1 0.0349 0 0 0 0.268 0.958 1 0 1 0.0349 0 0 0 0.319 0.958 1 0.028 0.972 0.0349 0 0.0809 0.0809 0.371 0.958 1 0.06 0.94 0.0349 0 0.116 0.116 0.423 0.958 1 0.128 0.872 0.0349 0 0.16 0.16 0.474 0.958 0.999 0.228 0.772 0.0349 0.00629 0.176 0.176 0.526 0.958 0.997 0.416 0.584 0.0349 0.00899 0.209 0.209 0.577 0.958 0.988 0.552 0.449 0.0349 0.0181 0.216 0.215 0.629 0.958 0.974 0.616 0.388 0.0349 0.03 0.201 0.197 0.681 0.958 0.964 0.664 0.343 0.0349 0.0345 0.196 0.189 0.732 0.958 0.952 0.692 0.318 0.0349 0.0392 0.186 0.18 0.784 0.958 0.931 0.728 0.291 0.0349 0.0465 0.165 0.154 0.835 0.958 0.896 0.824 0.228 0.0349 0.0447 0.149 0.118 0.887 0.958 0.832 0.932 0.206 0.0349 0.0506 0.119 0.0845 0.938 0.958 0.682 0.996 0.32 0.0349 0.07 0.0283 0.0687 0.99 0.958 0.172 1 0.828 0.0349 0.0604 0 0.0604 Tuning parameter 'mtry' was held constant at a value of 3 Dist was used to select the optimal model using the smallest value. The final values used for the model were mtry = 3 and threshold = 0.887.
results
Using ggplot(mod1) will show the performance profile. Instead here is a plot of the sensitivity, specificity, and distance to the perfect model:
library(reshape2) metrics <- mod1$results[, c(2, 4:6)] metrics <- melt(metrics, id.vars = "threshold", variable.name = "Resampled", value.name = "Data") ggplot(metrics, aes(x = threshold, y = Data, color = Resampled)) + geom_line() + ylab("") + xlab("Probability Cutoff") + theme(legend.position = "top")
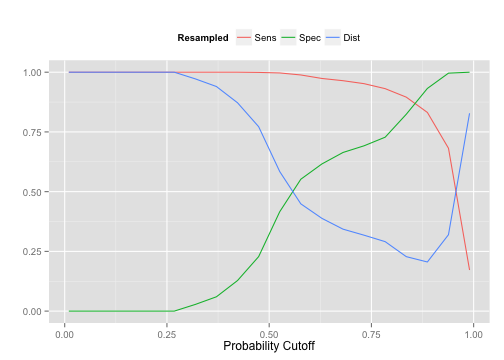
You can see that as we increase the probability cut off for the first class it takes more and more evidence for a sample to be predicted as the first class. As a result the sensitivity goes down when the threshold becomes very large. The upside is that we can increase specificity in the same way. The blue curve shows the distance to the perfect model. The value of 0.89 was found to be optimal.
Now we can use the test set ROC curve to validate the cut off we chose by resampling. Here the cut off closest to the perfect model is 0.83. We were able to find a good probability cut off value without setting aside another set of data for tuning the cut off.
One great thing about this code is that it will automatically apply the optimized probability threshold when predicting new samples.